Working through the literature for the book I’ve read this article and the results intrigued me. The authors analyzed the fees earned by liquiditiy providers as a function of fee levels, and their result was surprising. Paraphrasing it slightly it reads
When only considering arbitrage trades, the optimal fee level, ie the fee level with a maximum fee income for LPs, is as small as possible whilst not being zero
In other words, the result of their analysis is that the volume lost by increasing the fees more than outweighs the gains from higher fee levels. As said, this surprised me and whilst undoubtedly correct in their scenario - their analysis is excellent and unlikely to be wrong - the real world my introduce some additional constraints that negate the effect.
For reference, here my first twitter thread on this paper
for the book working my way through a number of papers and came across this one from @tarunchitra @alexhevans and @GuilleAngeris https://t.co/ENivUh6t0u
— Oscar D Þorson (@odtorson) January 8, 2022
and here the second, more detailed one
OK, so after the general horror show and the Brownian motion horror show, let's now come back to this paperhttps://t.co/ysoqpSS5rC
— Oscar D Þorson (@odtorson) January 9, 2022
Here just the key results in note format. As we discuss in the paper, when prices move from $x_1$ to $x_2$ (we assume $x_2 > x_1$ for simplicity of notations), ignoring fees a constant-product AMM allows trading at a price of $\sqrt{x_1 x_2}$. As the then market price is $x_2$ the arbitrageur’s profit, before fees, is
$$ P_0 = \frac{x_2}{\sqrt{x_1 x_2}}-1 = \sqrt \frac{x_2}{x_1} - 1 = \sqrt \rho - 1 $$
where $\rho = x_2/x_1$ is the ratio between old and new price.
This calculation assumed no fees, so we now introduce a percentage fee $\varphi$. This fee reduces the profit, and we find that the percentage profit after fees $P$ is
$$ P = P_0 - \varphi = \sqrt \rho - 1 - \varphi $$
If we look at break-evens, let’s assume $\varphi=1%$. To break even we must have $\sqrt \rho \geq 1.01$ or $\rho > 1.02$. So for a 1% fee we need a 2% move, and generally (for small moves) we find that the move must be at least double the fees for arbitrageurs to come in.
Total fees earned are proportional to the number of transactions that happen, and to the fee percentage. A Brownian motion progresses in time like $\sqrt{t}$ so initially it is extremely steep
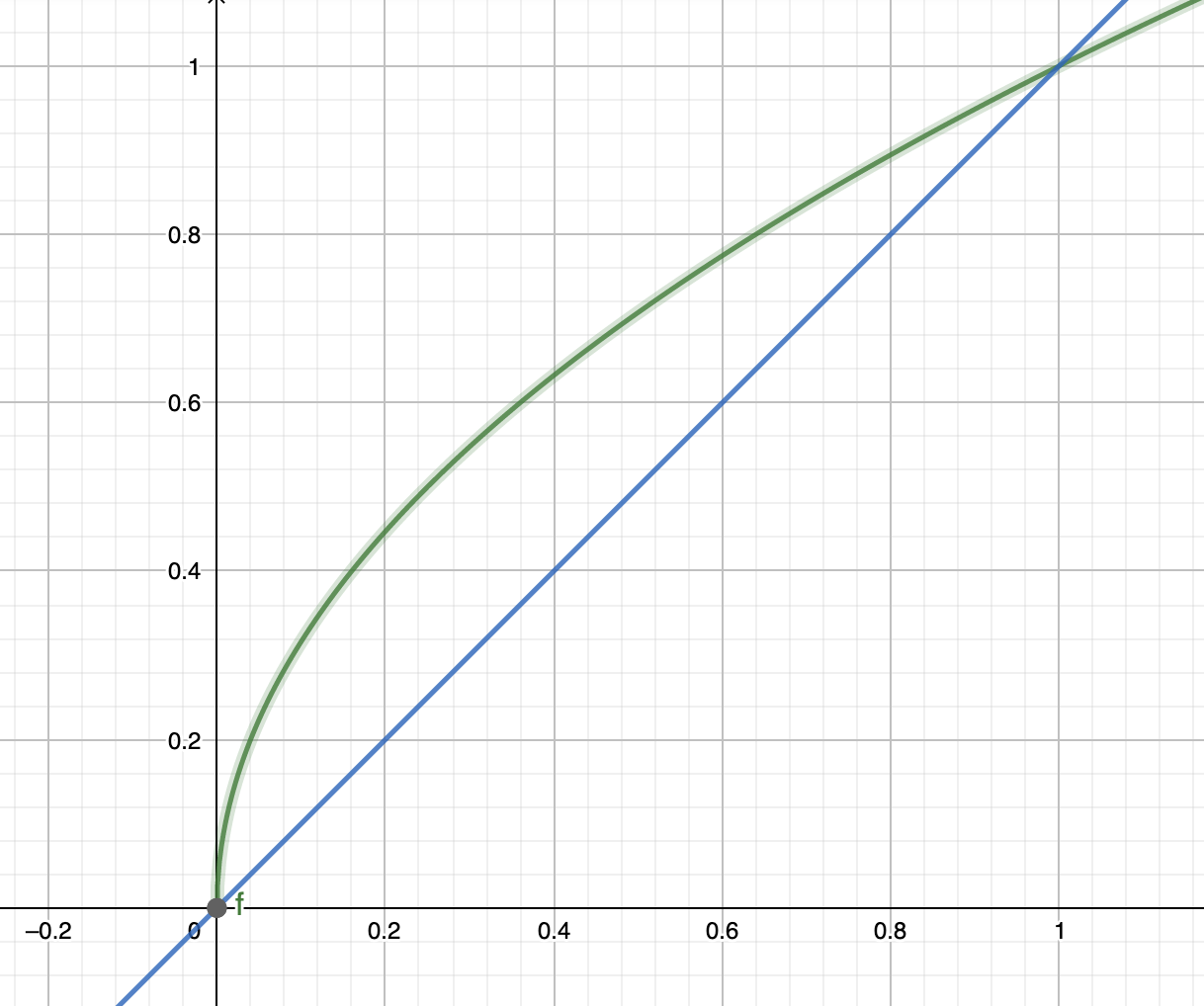
This means that if the fee is very small already and I decrease it even more, the impact of the decrease in fee percentage will be smaller than the impact of the increase in transactions. Note that this does not necessarily hold for bigger fee levels where the square root function gets flatter.
If we ignore customer trades the optimization is awkward – it appears that there might be two maximums, one with fees levels that are almost zero (where a decrease in fees massively increases trading volume), and one with fee levels that are very big (where an increase in fees does not strongly impact the trading volume).
The one towards very high fee levels is arguably not that desirable – there is a benefit of earning steady fees rather than going for the once-in-a-lifetime big fee event. On the low side we need to take into account other transaction costs like gas, and simply the fact that there is a limit to the frequency at which trades can happen, which would imply a finite rather than infinitesimal optimal fee level.
Note that overall this analysis is somewhat moot however: arbitrageur fees are nice, and it is a good idea to claw back some of the arbitrage gains via fees, but ultimately trading with arbitrageurs will never be profitable for an AMM – arbitrageurs by definition only trade if they can extract value.
The real question therefore is how the customer trades react to fee levels – and ultimately a quantitative estimate of this trade demand curve is arguably more pertinent for looking at optimal fee levels than is the fee levels that would be optimal were only arbitrageurs to trade on the AMM.
