Stable Swap

Key formulas

Characteristic function

$$ f_{\chi;k}(x,y) = \chi k (x+y)+xy = (\chi + \frac 1 4) \ k^2 $$

The parameter $\chi$ determines the shape of the curve: for $\chi=0$ it is a constant product curve, and for $\chi \to \infty$ the curve will converge towards the constant sum curve. The convergence is such that the “flat” range gets wider and wider and the curvature is pushed to the boundaries to ensure that the full price range is covered. The presence of $k$ within the formula for $f$ and the complex formula on the right ensure that $k$ scales linearly with the size of the pool.

The parameter $\chi$ is not constant but is adjusted dynamically depending on the composition of the pool: if both assets are perfectly balanced then $\chi$ is at its maximum value, and the more the pool moves ot one of the two boundaries the smaller gets $\chi$ and therefore the bigger gets the curvature. This encourages arbitrageurs to push the pool back towards a balanced state.

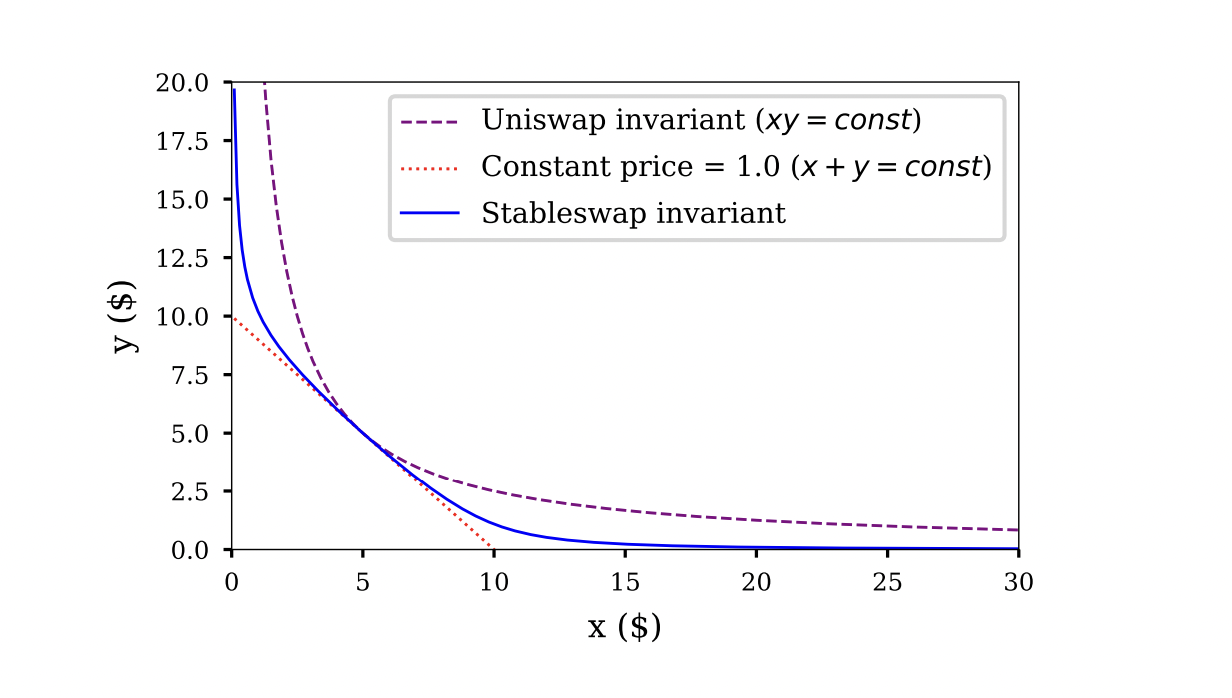
Indifference curve

$$ y_k(x) = \chi k (x+y)+xy = \frac {(4 \chi + 1) \ k^2} {4(\chi k + x)} $$

Note that this is the indifference curve at $\chi = const$. As $\chi$ changes when the pool composition $x$ changes this is only accurate to the extent that $\chi$ has not yet been adjusted.

---

Notes

The purpose of the stable swap curve is to trade like-kind assets, ie assets that by design have a fixed exchage rate like different stable coins that are linked to the same reference asset. A standard AMM, especially a constant product AMM, would be extremely inefficient for those as most of its liquidity would be available far outside the range of possible exchange ratios.

The stable swap curve is a combination of the constant sum curve and the constant product curve, combined using the curve parameter $\chi$. The combined curve is mostly flat, ie it is very close to flat for most states of the AMM. It is only at the boundaries, when the AMM runs out of one of the two assets, that the constant product part of the formula kicks in and the characteristic function gets significant curvature. Regardless of the parameter $\chi$ that controls the flatness of the curve, the asymptotic behaviour of the AMM is always such that it cover the whole price range, albeit across a smaller and smaller volume as $\chi$ increases (the curvature is pushed out to the boundaries).

Stableswap indifference curve from [Egorov19]

References

The main reference for stable swaps is [Egorov19]. Another good reference is [Feito20], and a more recent, alternative explanation is in [Feito21]. [Egorov21] takes this concept further to non like-kind assets.

Please see here for the full list of references.

---

Whilst reasonable care has been taken to verify the above formulas they may still contain errors. Please do not use them without independent verification.