Constant Product

Key formulas

Characteristic function

$$ f(x,y) = k = \sqrt{x*y} $$

Often the simpler yet equivalent function $f(x,y)=x*y$ is used. However, with the formula we have provided above, $k$ scales linearly with the size of the pool.

Indifference curve

$$ y = \frac{k^2}{x} $$

The fact that $k^2$ appears in the numerator and not another power of $k$ shows that $k$ scales like a currency.

Price response function

$$ \pi(x) = \frac{k^2}{x^2} = \frac{y(x)}{x} $$

The PRF is neither bounded from below nor from above, therefore the whole price range is covered and the AMM will never run out of either of the asset. Note the $\frac y x$ term which is very common for the various types of AMMs that rely on a product for the characteristic function.

AMM portfolio value

$$ \nu(\xi) = \sqrt{\xi} $$

The portfolio value of the AMM is in square root $x$, which is the profile that is generated by the always keep the same amount of value in both assets investment strategy. For moderate price movements (up to 20-50%) this strategy is reasonably linear, but it diverges dramatically for bigger price movements.

Divergence loss

$$ \Lambda(\xi) = \frac 1 2 (1 + \xi) - \sqrt \xi $$

The DL behaves like $\xi-\sqrt \xi$ which is reasonably small for not too big price movements (up to 20-50%). However, in case of massive divergence (eg 5-10x or more) a $\sqrt x$ portfolio massively underperforms a linear one.

Strike density function

$$ \mu(K) = -\frac{1}{4 K \sqrt K} $$

The constant product AMM profile has an infite strike density towards $K=0$, with a pole that grows like $K^{-\frac 3 2}$. The strike density function is negative because the profile is short option, ie the AMM is an option seller.

Cash strike density function

$$ \mu_{\mathbf{cash}}(K) = -\frac{1}{4 \sqrt K} $$

The cash strike density function also has a pole at $K=0$ and the pole is significantly more violent than the one of the regular strike density function.

Cash Gamma

$$ \Gamma_{\mathbf{cash}}(K) = -\frac{1}{4} \sqrt K $$

The cash Gamma of the constant product AMM is non-zero everywhere, but it is well behaved in that it does not have a pole at $K=0$. In fact, it goes to zero when $K \to 0$. It is non-zero everywhere, and negative, as the AMM is short an option.

---

Notes

The constant product AMM is the standard AMM introduced and popularized by Bancor and Uniswap. Its advantage is that it never runs out of assets, regardless the price. This also makes it an excellent price oracle. Its disadvantage is that it can suffer a significant divergence losses if prices diverge a lot (2x or more). Also it is not very efficient in terms of the collateral deployed as most of it is used to make markets far away from the current price. As a consequence, slippage per unit of liquidity is higher than for more optimised models.

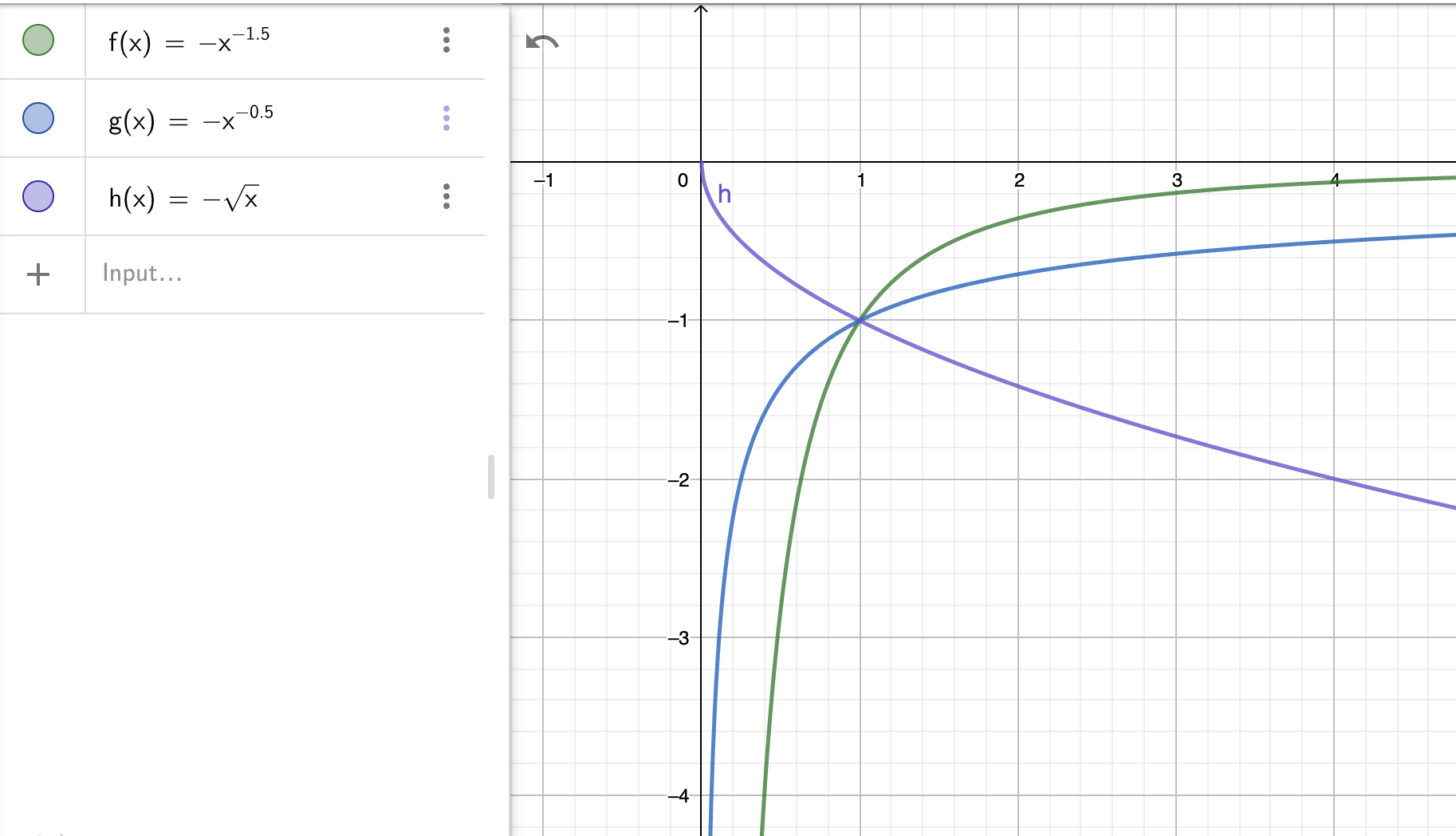
In the chart below we plot the strike density function (green), the cash strike density function (blue), and the cash gamma. Those curves are all negative as the AMM is short options. The strike density function diverges for $\xi\to 0$, therefore complete replication is not possible. However, Cash Gamma disappears on the downside so the AMM behaves reasonably well.

---

Whilst reasonable care has been taken to verify the above formulas they may still contain errors. Please do not use them without independent verification.