Constant Sum

Key formulas

Characteristic function

$$ f(x,y) = k = p_0\cdot x+y $$

The parameter $p$ is the (constant) price that is being offered by this AMM.

Indifference curve

$$ y = k - p_0\cdot x $$

The indifference curve of this AMM is a straight line sloping downwards.

Price response function

$$ \pi(x) = p_0 $$

The AMM exclusively operates at the constant price $p_0$.

AMM portfolio value

$$ \nu_{p_0}(p) \simeq \min(p, p_0) $$

The equilibrium state of the AMM does not provide an indication for the current market price, so the porfolio value can not be read from the AMM state. This is similar to a range-bound AMM outside of the range; in fact - the constant sum AMM can be considered a range-bound AMM with a very narrow range.

Assuming the market price is at $p$, then the portfolio is 100% in the numeraire if $p>p_0$, and 100% in the risk asset if $p<p_0$. Therefore, whenever the price diverges from $p_0$ the AMM is 100% in the underperforming asset that it has acquired at par. The normalization in the above formula is that the AMM holds 1 unit of the risk asset.

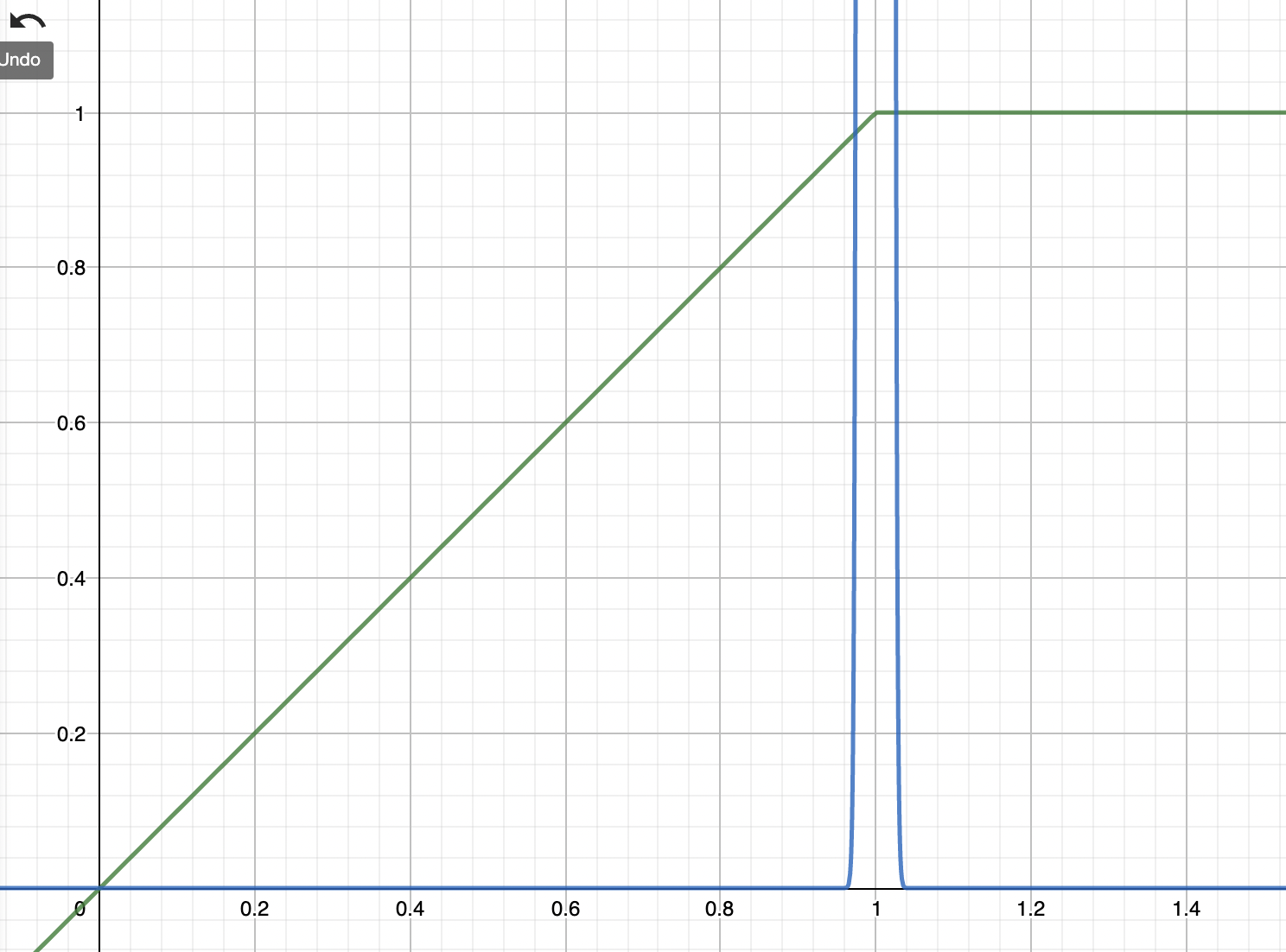
Note that the above profile effectively describes a short put option profile plus a bond (see chart below).

Strike density function

$$ \mu(K) = -\delta(K-p_0) $$

There is no convexity outside the price range, and the range itself is infinitesimally small at $p_0$. The strike density function is therefore a Kronecker delta “function”, ie a function (in the physicist sense) that has surface 1, is infinite at zero, and zero everywhere else. In other words: the density is that of a short strike at $K=p_0$

Cash strike density function

$$ \mu_{\mathbf{cash}}(K) = -p_0\ \delta(K-p_0) $$

In principle this would be $K \delta(K-p_0)$ but we used a property of the Kronecker delta to rewrite the above function.

Cash Gamma

$$ \Gamma_{\mathbf{cash}}(K) = -p_0^2\ \delta(K-p_0) $$

Again we used the property of the Kronecker delta to rewrite the formula, and again this is the cash Gamma of a short strike at $K=p_0$.

Divergence loss

$$ na $$

Divergence loss is not meaningful as there is no natural reference portfolio. However, the position still has negative convexity – is short an option – so there will be underperformance against any linear portfolio when the price is crossed.

---

Notes

The constant-sum AMM in this particular form is not very useful. Its main interest lies in its theoretical analysis. The reason is that it stands ready to buy and sell its entire liquidity portfolio at the fixed price $p$, so whenever the market price deviates from $p$ (which will almost always be the case) the AMM is in a border-state where 100% of the portfolio is in one of the two constituent assets.

For a more useful version of this AMM where the curve is only flat in the center but where there is some curvature at the boundaries to ensure the AMM stays within the range see the stableswap AMM.

The chart below shows the stylized profile of the portfolio value function which is a short put at $K=p_0$ plus a bond (or alternatively a call spread at $K=0$ and $K=p_0$). The blue curve indicates the Kronecker delta function at $p_0$ - infinitely high, infinitesimally thin, and surface 1.

---

Whilst reasonable care has been taken to verify the above formulas they may still contain errors. Please do not use them without independent verification.